Python: Count the number of equal numbers from three given integers

Python Basic - 1: Exercise-86 with Solution

Count Equal Numbers

Write a Python program to count the number of equal numbers from three given integers.

Sample Solution:

Python Code:

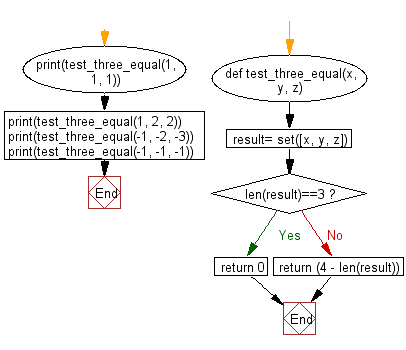
# Define a function named test_three_equal that takes three arguments: x, y, and z.
def test_three_equal(x, y, z):
    # Create a set containing the unique values of x, y, and z.
    result = set([x, y, z])

    # Check if the length of the set is equal to 3.
    if len(result) == 3:
        # If the set contains three unique values, return 0.
        return 0
    else:
        # If the set does not contain three unique values, return the difference between 4 and the set length.
        return (4 - len(result))

# Test the function with different sets of values and print the results.
print(test_three_equal(1, 1, 1))    
print(test_three_equal(1, 2, 2))    
print(test_three_equal(-1, -2, -3)) 
print(test_three_equal(-1, -1, -1))

Sample Output:

3
2
0
3

Explanation:

Here is a breakdown of the above Python code:

• Function Definition:
• The code defines a function named "test_three_equal()" that takes three arguments: 'x', 'y', and 'z'.
• Create a Set:
• Inside the function, a set named 'result' is created using the "set()" function, containing the unique values of 'x', 'y', and 'z'.
• Conditional Check:
• The code checks if the length of the set (len(result)) is equal to 3.
• Return Statements:
• If the set contains three unique values, the function returns 0.
• If the set does not contain three unique values, the function returns the difference between 4 and the set length ((4 - len(result))).

Pictorial Presentation:

Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to check whether a given string is an "isogram" or not.
Next: Write a Python program to check whether a given employee code is exactly 8 digits or 12 digits.