Python Math: Get the nth tetrahedral number from a given integer(n) value
Python Math: Exercise-84 with Solution
A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron. The formula for the nth tetrahedral number is represented by the 3rd rising factorial of n divided by the factorial of 3:
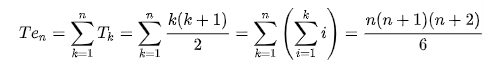
Example of tetrahedral numbers:
| N | Tetrahedral Number |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 10 |
| 4 | 20 |
| 5 | 35 |
| 6 | 56 |
Write a Python program to get the nth tetrahedral number from a given integer(n) value.
Sample Solution:
Python Code:
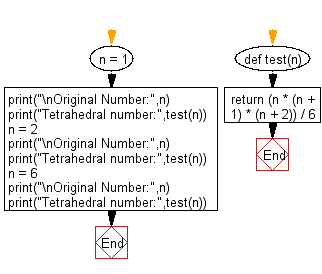
def test(n):
return (n * (n + 1) * (n + 2)) / 6
n = 1
print("\nOriginal Number:",n)
print("Tetrahedral number:",test(n))
n = 2
print("\nOriginal Number:",n)
print("Tetrahedral number:",test(n))
n = 6
print("\nOriginal Number:",n)
print("Tetrahedral number:",test(n))
Sample Output:
Original Number: 1 Tetrahedral number: 1.0 Original Number: 2 Tetrahedral number: 4.0 Original Number: 6 Tetrahedral number: 56.0
Flowchart:
Visualize Python code execution:
The following tool visualize what the computer is doing step-by-step as it executes the said program:
Python Code Editor:
Have another way to solve this solution? Contribute your code (and comments) through Disqus.
Previous: Write a Python program to calculate the aliquot sum of an given integer.
Next: Write a Python program to get the sum of the powers of all the numbers from start to end (both inclusive).
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
Python: Tips of the Day
Lambdas for Sorting:
>>> students = [{'name': 'John', 'score': 98}, {'name': 'Mike', 'score': 94}, {'name': 'Jennifer', 'score': 99}]
>>> sorted(students, key=lambda x: x['score'])
[{'name': 'Mike', 'score': 94}, {'name': 'John', 'score': 98}, {'name': 'Jennifer', 'score': 99}]
- Exercises: Weekly Top 12 Most Popular Topics
- Pandas DataFrame: Exercises, Practice, Solution
- Conversion Tools
- JavaScript: HTML Form Validation
- SQL Exercises, Practice, Solution - SUBQUERIES
- C Programming Exercises, Practice, Solution : For Loop
- Python Exercises, Practice, Solution
- Python Data Type: List - Exercises, Practice, Solution
- C++ Basic: Exercises, Practice, Solution
- SQL Exercises, Practice, Solution - exercises on Employee Database
- SQL Exercises, Practice, Solution - exercises on Movie Database
- SQL Exercises, Practice, Solution - exercises on Soccer Database
- C Programming Exercises, Practice, Solution : Recursion