Python Exercise: Check whether a number is perfect or not

Last update on April 22 2025 12:58:08 (UTC/GMT +8 hours)

11. Check if a Number is Perfect

Write a Python function to check whether a number is "Perfect" or not.

According to Wikipedia : In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself (also known as its aliquot sum). Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself).
Example : The first perfect number is 6, because 1, 2, and 3 are its proper positive divisors, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) / 2 = 6. The next perfect number is 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128.

Sample Solution:

Python Code:

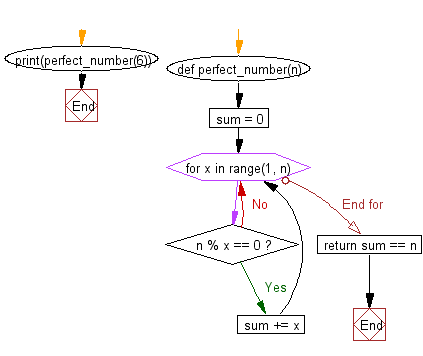
# Define a function named 'perfect_number' that checks if a number 'n' is a perfect number
def perfect_number(n):
    # Initialize a variable 'sum' to store the sum of factors of 'n'
    sum = 0
    
    # Iterate through numbers from 1 to 'n-1' using 'x' as the iterator
    for x in range(1, n):
        # Check if 'x' is a factor of 'n' (divides 'n' without remainder)
        if n % x == 0:
            # If 'x' is a factor of 'n', add it to the 'sum'
            sum += x
    
    # Check if the 'sum' of factors is equal to the original number 'n'
    return sum == n

# Print the result of checking if 6 is a perfect number by calling the 'perfect_number' function
print(perfect_number(6))

Sample Output:

True

Explanation:

In the exercise above the code defines a function named "perfect_number()" that determines whether a given number 'n' is a perfect number. It iterates through numbers from 1 to 'n-1' to find factors of 'n' and calculates their sum. Finally, it checks if the sum of factors is equal to the original number 'n' and prints the result (True if 'n' is a perfect number, False otherwise) for the number 6.

Pictorial presentation:

Python exercises: Check whether a number is perfect or not.

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python function that computes the sum of proper divisors of a number and checks if it equals the number.
Write a Python function that uses a loop to find all proper divisors of a number and then compares the sum to the number.
Write a Python function that implements a generator to yield proper divisors and then sums them to determine if the number is perfect.
Write a Python function that uses list comprehension to gather divisors and check if the number is perfect, handling edge cases like 1.

Go to:

Previous: Write a Python program to print the even numbers from a given list.
Next: Write a Python function that checks whether a passed string is palindrome or not.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.