NumPy Statistics: Mean, Median, Covariance Exercises
This resource offers a total of 70 NumPy Statistics problems for practice. It includes 14 main exercises, each accompanied by solutions, detailed explanations, and four related problems.
The following exercises demonstrate how to perform a diverse range of statistical and analytical operations using NumPy, including computing extrema, percentiles, medians, and weighted averages, as well as analyzing correlations and generating histograms.
[An Editor is available at the bottom of the page to write and execute the scripts.]
1. Maximum and Minimum of Flattened Array
Write a Python program to find the maximum and minimum value of a given flattened array.
Expected Output:
Original flattened array:
[[0 1]
[2 3]]
Maximum value of the above flattened array:
3
Minimum value of the above flattened array:
0
Click me to see the sample solution
2. Minimum and Maximum Along Second Axis
Write a NumPy program to get the minimum and maximum value of a given array along the second axis.
Expected Output:
Original array:
[[0 1]
[2 3]]
Maximum value along the second axis:
[1 3]
Minimum value along the second axis:
[0 2]
Click me to see the sample solution
3. Range (Difference Between Max and Min) Along Second Axis
Write a NumPy program to calculate the difference between the maximum and the minimum values of a given array along the second axis.
Expected Output:
Original array:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
Difference between the maximum and the minimum values of the said array:
[5 5]
Click me to see the sample solution
4. 80th Percentile Along Second Axis
Write a NumPy program to compute the 80th percentile for all elements in a given array along the second axis.
Expected Output:
Original array:
[1.0, 2.0, 3.0, 4.0]
Largest integer smaller or equal to the division of the inputs:
[ 0. 1. 2. 2.]
Click me to see the sample solution
5. Median of Flattened Array
Write a NumPy program to compute the median of flattened given array.
Note: First array elements raised to powers from second array
Expected Output:
Original array:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
Median of said array:
5.5
Click me to see the sample solution
6. Weighted Average of an Array
Write a NumPy program to compute the weighted of a given array.
Sample Output:
Original array:
[0 1 2 3 4]
Weighted average of the said array:
2.6666666666666665
Click me to see the sample solution
7. Mean, Standard Deviation, and Variance Along Second Axis
Write a NumPy program to compute the mean, standard deviation, and variance of a given array along the second axis.
Sample output:
Original array:
[0 1 2 3 4 5]
Mean: 2.5
std: 1
variance: 2.9166666666666665
Click me to see the sample solution
8. Covariance Matrix of Two Arrays
Write a NumPy program to compute the covariance matrix of two given arrays.
Sample Output:
Original array1:
[0 1 2]
Original array1:
[2 1 0]
Covariance matrix of the said arrays:
[[ 1. -1.]
[-1. 1.]]
Click me to see the sample solution
9. Cross-Correlation of Two Arrays
Write a NumPy program to compute cross-correlation of two given arrays.
Sample Output:
Original array1:
[0 1 3]
Original array1:
[2 4 5]
Cross-correlation of the said arrays:
[19]
Click me to see the sample solution
10. Pearson Product-Moment Correlation Coefficients
Write a NumPy program to compute pearson product-moment correlation coefficients of two given arrays.
Sample Output:
Original array1:
[0 1 3]
Original array1:
[2 4 5]
Pearson product-moment correlation coefficients of the said arrays:
[[1. 0.92857143]
[0.92857143 1. ]]
Click me to see the sample solution
11. Element-wise Finite/Infinite/NaN Checks
Write a NumPy program to test element-wise of a given array for finiteness (not infinity or not Not a Number), positive or negative infinity, for NaN, for NaT (not a time), for negative infinity, for positive infinity.
Sample output:
Test element-wise for finiteness (not infinity or not Not a Number):
True
True
False
Test element-wise for positive or negative infinity:
True
False
True
Test element-wise for NaN:
[ True False False]
Test element-wise for NaT (not a time):
[ True False]
Test element-wise for negative infinity:
[1 0 0]
Test element-wise for positive infinity:
[0 0 1]
Click me to see the sample solution
12. Weighted Average Along Specified Axis of a Flattened Array
Write a Python NumPy program to compute the weighted average along the specified axis of a given flattened array.
From Wikipedia: The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics.
Sample output:
Original flattened array:
[[0 1 2]
[3 4 5]
[6 7 8]]
Weighted average along the specified axis of the above flattened array:
[1.2 4.2 7.2]
Click me to see the sample solution
13. Count Occurrences Using bincount
Write a Python program to count number of occurrences of each value in a given array of non-negative integers.
Note: bincount() function count number of occurrences of each value in an array of non-negative integers in the range of the array between the minimum and maximum values including the values that did not occur.
Sample Output:
Original array:
[0, 1, 6, 1, 4, 1, 2, 2, 7]
Number of occurrences of each value in array:
[1 3 2 0 1 0 1 1]
Click me to see the sample solution
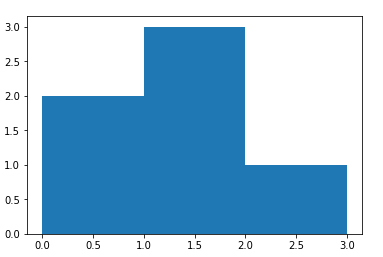
14. Compute Histogram of Data Against Bins
Write a NumPy program to compute the histogram of nums against the bins.
Sample Output:
nums: [0.5 0.7 1. 1.2 1.3 2.1]
bins: [0 1 2 3]
Result: (array([2, 3, 1], dtype=int64), array([0, 1, 2, 3]))
Click me to see the sample solution
Python-Numpy Code Editor:
More to Come !Do not submit any solution of the above exercises at here, if you want to contribute go to the appropriate exercise page.
Test your Python skills with w3resource's quiz
