HTML5 Canvas arcs tutorial

Last update on August 19 2022 21:50:55 (UTC/GMT +8 hours)

Drawing arcs

You can draw arcs on canvas using the arc() method. Before going details on drawing arcs, here's a brief overview on radian and angle :

The radian is the standard unit of angular measure, used in many areas of mathematics. An angle's measurement in radians is numerically equal to the length of a corresponding arc of a unit circle, so one radian is just under 57.3 degrees (when the arc length is equal to the radius). The radian is represented by the symbol rad An alternative symbol is the superscript letter c. So for example, a value of 1.3 radians could be written as 1.3 rad or 1.3^c. See the following diagram :

Use the following formula to convert degrees to radians:

var radians = degrees * Math.PI/180

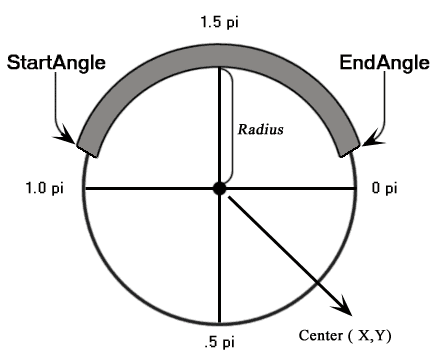
arc Method: arc(x, y, radius, startAngle, endAngle, direction)

Parameters	Type	Description
x	number	The x-coordinate (in pixels), for the center point of the arc in relation to the upper-left corner of the canvas rectangle.
y	number	The y-coordinate ( in pixels), for the center point of the arc in relation to the upper-left corner of the canvas rectangle.
radius	number	The radius or distance from the point (x,y) that the arc's path follows.
startAngle	number	The starting angle, in radians, clockwise, with 0 corresponding to the 3:00 o’clock position on the right of the circle.
endAngle	number	The ending angle, in radians.
direction	bool	true : The arc is drawn in a counterclockwise direction from start to end. false : The arc is drawn in a clockwise direction from start to end.

Example : HTML5 Canvas arc using arc() method

The following web document creates a simple arc.

Output :

simple arc

Code:

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title></head>
<body>
<canvas id="demoCanvas" width="340" height="340"> canvas</canvas> 
<script>
var canvas = document.getElementById('demoCanvas');
var ctx = canvas.getContext('2d');
var x = 90;
var y = 100;
var radius = 75;
var startAngle = 1.1 * Math.PI;
var endAngle = 1.9 * Math.PI;
var counterClockwise = false;
ctx.beginPath();
ctx.arc(x, y, radius, startAngle, endAngle, counterClockwise);
ctx.lineWidth = 10;
// line color
ctx.strokeStyle = 'green';
ctx.stroke();
</script>
</body> 
</html>

Example : HTML5 Canvas miscellaneous arcs

The following web document creates various types of arcs.

Output :

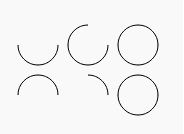
Miscellaneous arcs

Code :

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title>
<script type="text/javascript">  
function misc_curves()
 {
    var canvas = document.getElementById("Mycanvas");
    if (canvas.getContext) 
	 {
	   var context = canvas.getContext("2d");
	     for (var i = 0; i < 2; i++)                            
		 // Step through two rows.
		  {
		 // Step through three versions.        
		 for (var j = 0; j < 3; j++)                        
	       {
		     context.beginPath();
			// The x-coordinate.
			 var x = 35 + j * 50;  
		    // The y-coordinate.    
			 var y = 35 + i * 50;            
		   // The arc radius.    
		     var radius = 20;  
	       // The starting point on the circle.    
		     var startAngle = 0;                     
	      //end point on the circle.    
		     var endAngle = Math.PI + (Math.PI * j) / 2; 
	      // The direction of drawing.    
		     var anticlockwise = i % 2 === 0 ? false : true; 
		  // Create the arc path.   
		    context.arc(x, y, radius, startAngle, endAngle, anticlockwise); 
	     // Show the arcs
		    context.stroke();                               
        }
		 }  
     }
}
</script>  
</head>
<body onload="misc_curves();">
<canvas id="Mycanvas" width="340" height="340"> canvas</canvas> 
</body> 
</html>

Drawing Circles

An arc is a part of a circle. To draw a circle, draw an arc with a starting angle of 0 and ending angle of 2 x Pi. Here is an example :

Output :

Code :

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title></head>
<body>
<canvas id="demoCanvas" width="340" height="340"> canvas</canvas> 
<script>
var canvas = document.getElementById('demoCanvas');
var ctx = canvas.getContext('2d');
var x = 90;
var y = 100;
var radius = 75;
var startAngle = 0;
var endAngle = 2 * Math.PI;
var counterClockwise = false;
ctx.beginPath();
ctx.arc(x, y, radius, startAngle, endAngle, counterClockwise);
ctx.lineWidth = 10;
// line color
ctx.strokeStyle = 'blue';
ctx.stroke();
</script>
</body> 
</html>

arcTo Method: arcTo(x1, y1, x2, y2, radius)

The arcTo() method creates an arc of radius between two tangents. The first tangent is defined by an imaginary line that is drawn through the last point in a path and the point (x1, y1). The second tangent is defined by an imaginary line that is drawn through the point (x1, y1) and the point (x2, y2).

Syntax :
arcTo(x1, y1, x2, y2, radius);

Parameters	Type	Description
x1	number	The x-coordinate for the first tangent that intersects with the current path point.
y1	number	The y-coordinate for the first tangent that intersects with the current point.
x2	number	The x-coordinate for the second tangent that intersects with the x1 and y1 points.
y2	number	The y-coordinate for the second tangent that intersects with the x1 and y1 points.
radius	number	The radius of the arc to create.

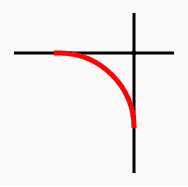
Example : HTML5 Canvas arcTo() method

The following web document creates a rounded corner between a horizontal and a vertical line.

Output :

Code :

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title></head>
<body>
<canvas id="myCanvas" width="300" height="600"></canvas>
<script>
var canvas = document.getElementById("myCanvas");
if (canvas.getContext) 
{
var ctx = canvas.getContext("2d");
// Draw the imaginary tangents in blue.
ctx.beginPath();
ctx.lineWidth = "3";
ctx.strokeStyle = "black";
ctx.moveTo(80, 100);
ctx.lineTo(240, 100);
ctx.moveTo(200, 60);
ctx.lineTo(200, 220);
ctx.stroke();         
// Draw it.
// Create two lines that have a connecting arc that could be used as a start to a rounded rectangle.
ctx.beginPath();
ctx.strokeStyle = "red";
ctx.lineWidth = "5";
ctx.moveTo(120, 100);   // Create a starting point.
ctx.arcTo(200, 100, 200, 220, 75); // Create an arc.
ctx.stroke(); 
}
</script>
</body> 
</html>

HTML5 Canvas : Drawing Bezier Curves

Bezier curves are used in computer graphics to produce curves which appear reasonably smooth at all scales. Originally developed by Pierre Bézier in the 1970's for CAD/CAM operations. In vector graphics, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths," as they are commonly referred to in image manipulation programs, are combinations of linked Bézier curves. Bézier curves are also used in animation as a tool to control motion

You can draw bezier curves in the same way as you draw lines, but instead of using the lineTo() method, you use either the bezierCurveTo() method or quadraticCurveTo() method. bezierCurveTo() method connects the endpoints with a cubic bezier curve using a specified pair of control points and the quadraticCurveTo() method connects the endpoints with a quadratic bezier curve using a single specified control point.

bezierCurveTo() method

A cubic Bézier curve must include three points. The first two points (cp1x,cp1y) and (cp2x, cp2y) are control points that are used in the cubic Bézier calculation and the last point (x,y) is the ending point for the curve.

Syntax:
bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)

Parameters	Type	Description
cp1x	number	The x-coordinate of the first Bézier control point.
cp1y	number	The y-coordinate of the first Bézier control point.
cp2x	number	The x-coordinate of the second Bézier control point.
cp2y	number	The y-coordinate of the second Bézier control point.
x	number	The x-coordinate of the point to add to the current path.
y	number	The y-coordinate of the point to add to the current path.

Note : The first point on the curve is the last point in the existing current subpath. If a path does not exist, use the beginPath and moveTo methods to create a starting point.

See the following diagram :

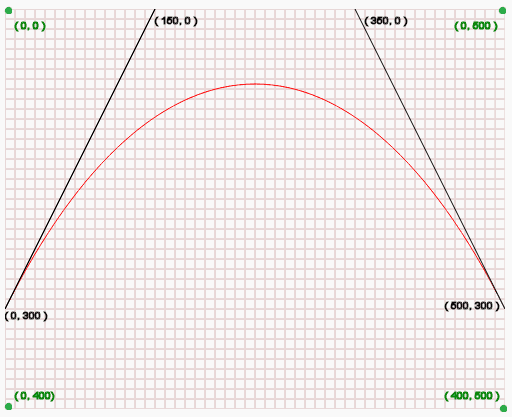
In the above diagram :

(0, 0) is the top-left position of the canvas.
(0, 400) is the bottom-left position of the canvas.
(0, 500) is the top-right position of the canvas.
(400, 500) is the bottom-right position of the canvas.
(0, 300) is the starting point of the curve.
(150, 0) i.e. (cp1x, cp1y) is the first control position of the curve.
(350, 0) i.e. (cp2x, cp2y) is the second control position of the curve.
(500, 300) i.e. (x, y) is the ending point of the curve.

Example : HTML5 Canvas Bezier Curve using bezierCurveTo() method

The following web document draws some straight lines and a Bézier curve (between two points) and creates the character 'R'.

Output :

Code :

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title></head>
<body>
<canvas id="DemoCanvas" width="500" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
var ctx = canvas.getContext("2d");
ctx.lineWidth = 7;
ctx.lineCap = "round";
ctx.clearRect(0, 0, canvas.width, canvas.height);
ctx.beginPath();
ctx.moveTo(30, 200);
ctx.lineTo(30, 50);
ctx.lineTo(65, 50);
ctx.moveTo(30, 120);
ctx.lineTo(65, 120);
ctx.lineTo(100, 200);
ctx.strokeStyle = "black";
ctx.stroke();
ctx.beginPath();
ctx.moveTo(65, 50);
ctx.bezierCurveTo(120, 50, 120, 120, 65, 120);
ctx.strokeStyle = "green";
ctx.stroke();
</script>
</body> 
</html>

quadraticCurveTo() method

A quadratic Bézier curve requires two points. The first point is a control point that is used in the quadratic Bézier calculation and the second point is the ending point for the curve.

Syntax :
quadraticCurveTo(cp1x, cp1y, x, y);

Parameters	Type	Description
cp1x	number	The x-coordinate of the Bézier control point.
cp1y	number	The y-coordinate of the Bézier control point.
x	number	The x-coordinate of the point to add to the current path.
y	number	The y-coordinate of the point to add to the current path.

Note : The starting point for the curve is the last point in the existing current subpath. If a path does not exist, use beginPath() and moveTo() methods to set a starting point.

See the following diagram :

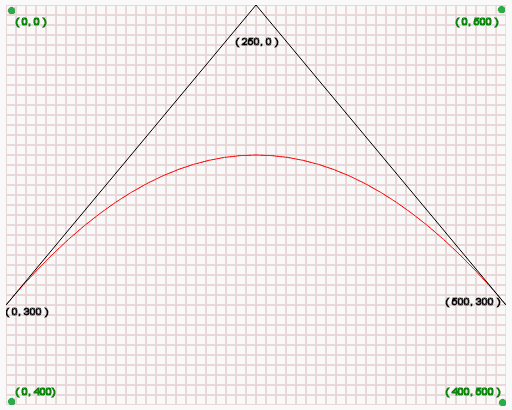
In the above diagram :

(0, 0) is the top-left position of the canvas.
(0, 400) is the bottom-left position of the canvas.
(0, 500) is the top-right position of the canvas.
(400, 500) is the bottom-right position of the canvas.
(0, 300) is the starting point of the curve.
(250, 0) i.e. (cp1x, cp1y) is the control position of the curve.
(500, 300) i.e. (x, y) is the ending point of the curve.

Example : HTML5 Canvas quadratic Bezier Curve using quadraticCurveTo() method

In this example, six shapes together create the following graphics.

Output :

Code :

<!DOCTYPE html>
<html>
<head>
<title>Sample arcs example</title></head>
<body>
<canvas id="DemoCanvas" width="500" height="400"></canvas>
<script>
var canvas = document.getElementById('DemoCanvas');
  if (canvas.getContext)
  {
    var ctx = canvas.getContext('2d');
    // Draw shapes
    ctx.beginPath();
    ctx.moveTo(75,25);
    ctx.quadraticCurveTo(25,25,25,62.5);
    ctx.quadraticCurveTo(25,100,50,100);
    ctx.quadraticCurveTo(50,120,30,125);
    ctx.quadraticCurveTo(60,120,65,100);
    ctx.quadraticCurveTo(125,100,125,62.5);
    ctx.quadraticCurveTo(125,25,75,25);
    ctx.lineWidth = "3";
    ctx.strokeStyle = "green";
    ctx.stroke();
  } else {
    alert('Not supported in this browser.');
  }
</script>
</body> 
</html>

See the Pen html css common editor by w3resource (@w3resource) on CodePen.

Previous: HTML5 Canvas Line
Next: HTML5 Canvas path tutorial