HTML5 Canvas : Matrix Transforms

Last update on March 13 2024 14:37:44 (UTC/GMT +8 hours)

Introduction

Rotation, translation, and scaling are all accomplished using a transformation matrix—a set of nine numbers that are used to transform a two-dimensional array, such as a bitmap, using linear algebra. Mathematically, all transformations can be represented as 3x3 transformation matrices of the following form :

Since only six values are used in the above 3x3 matrix, a transformation matrix is also expressed as a vector: [a b c d e f].

Transformations map coordinates and lengths from a new coordinate system into a previous coordinate system

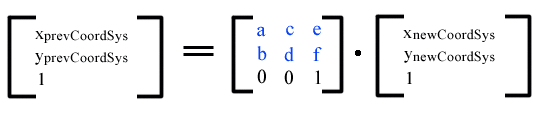
Simple transformations are represented in matrix form as follows :

Translation is equivalent to the matrix -

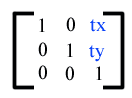
or [1 0 0 1 tx ty], where tx and ty are the distances to translate coordinates in X and Y, respectively.

Scaling is equivalent to the matrix -

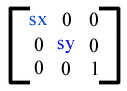
:or [sx 0 0 sy 0 0], One unit in the X and Y directions in the new coordinate system equals sx and sy units in the previous coordinate system, respectively.

Rotation about the origin is equivalent to the matrix -

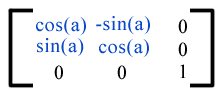
or [cos(a) sin(a) -sin(a) cos(a) 0 0], which has the effect of rotating the coordinate system axes by angle a.

A skew transformation along the x-axis is equivalent to the matrix -

or [1 0 tan(a) 1 0 0], which has the effect of skewing X coordinates by angle a.

A skew transformation along the y-axis is equivalent to the matrix -

You can reposition the origin (0,0) of your drawing surface by calling the translate(x,y) method. The origin of the canvas’s coordinate system is moved to the point (x,y). Using context’s rotate(angle) method you can rotate the canvas’s coordinate system around its origin. The coordinate system is rotated by angle radians, clockwise. Anything already on the canvas is unaffected, but subsequent drawing operations are rotated. The advantage of these methods is that the scaling will not simply multiple pixels.
These basic transform methods actually are affine transformations, calculated with matrics, with each new transformations bringing a new transformation to the previous matrix. You can define your own matrices with the following.

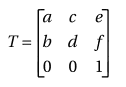
This is done with one of the following methods :

transform(a, b, c, d, e, f)
setTransform(a, b, c, d, e, f)

Note : The arguments a, b, c, d, e, and f are sometimes called m11, m12, m21, m22, dx, and dy or m11, m21, m12, m22, dx, and dy.

transform() method

The transform() method is used to modify the transformation matrix of the current context.

Syntax :

ctx.transform(m11, m12, m21, m22, dx, dy)

Parameters	Type	Description
m11	number	The m1,1 value in the matrix. [Increases or decreases the size of the pixels horizontally.]
m12	number	The m1,2 value in the matrix. [This effectively angles the X axis up or down.]
m21	number	The m2,1 value in the matrix. [This effectively angles the Y axis left or right.]
m22	number	The m2,2 value in the matrix. [Increases or decreases the size of the pixels vertically.]
dx	number	The delta x (dx) value in the matrix. [Moves the whole coordinate system horizontally]
dy	number	The delta y (dy) value in the matrix. [Moves the whole coordinate system vertically.]

setTransform () method

The setTransform(a, b, c, d, e, f) method reset the current transform to the identity matrix, and then invoke the transform(a, b, c, d, e, f) method with the same arguments.

Syntax:

ctx.setTransform(m11, m12, m21, m22, dx, dy)

Parameters	Type	Description
m11	number	The m1,1 value in the matrix. [Increases or decreases the size of the pixels horizontally.]
m12	number	The m1,2 value in the matrix. [This effectively angles the X axis up or down.]
m21	number	The m2,1 value in the matrix. [This effectively angles the Y axis left or right.]
m22	number	The m2,2 value in the matrix. [Increases or decreases the size of the pixels vertically.]
dx	number	The delta x (dx) value in the matrix. [Moves the whole coordinate system horizontally]
dy	number	The delta y (dy) value in the matrix. [Moves the whole coordinate system vertically.]

We have already discussed, rotation, translation, and scaling are all accomplished using a transformation matrix. See the following two examples, each example will draw a similar rectangle:

Example - 1:
The following web document draws a rectangle using transform() method :

Output:

Code:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.beginPath();  
 ctx.lineWidth = "3";  
 var cos=Math.cos(45*Math.PI / 180);
 var sin=Math.cos(45*Math.PI / 180);
 ctx.transform(cos, sin, -sin, cos, 160, 20); 
 ctx.strokeStyle = "red";  
 ctx.strokeRect(60, 60, 160, 160);  
 ctx.stroke();   
}
</script>
</body> 
</html>

Example - 2:
The following web document draws a similar rectangle of the previous example using translate() and rotate() methods :

Output:

Code :

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms and translate() and rotate() methods</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.beginPath();  
 ctx.translate(160, 20);   
 ctx.rotate(45*Math.PI / 180);
 ctx.strokeStyle = "red";  
 ctx.strokeRect(60, 60, 160, 160);  
 ctx.stroke();   
}
</script>
</body> 
</html>

Setting the Matrix for Reflection

Calling ctx.setTransform(1, 0, 0, -1, 0, 0) method you can set the transformation matrix to reflect everything around the y-axis. Therefore all drawing operations result in an upside-down image, and all y-coordinates are multiplied by -1.

Calling ctx.setTransform(-1, 0, 0, 1, 0, 0) method you can set up a transformation matrix to reflect everything around the x-axis. Therefore all drawing operations result in a mirror image, and all x-coordinates are multiplied by -1.

In the following example, all text reflected around the y-axis.

Output :

Code :




<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="150"></canvas>
<script>

var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) {
    var ctx = canvas.getContext('2d');
    ctx.font = "40px Arial";
    // Function to draw text with reflection
    function drawReflectedText(text, x, y, originalColor, reflectionColor) {
        // Measure the width and height of the text
        var textWidth = ctx.measureText(text).width;
        var textHeight = parseInt(ctx.font);
        // Draw reflection text
        ctx.fillStyle = reflectionColor;
        ctx.save(); // Save the current state of the context
        ctx.scale(1, -1); // Scale vertically by -1 to flip
        ctx.fillText(text, x, -(y + textHeight - 40)); // Draw reflected text immediately below the original
        ctx.restore(); // Restore the saved state to not affect other drawings
        // Draw original text
        ctx.fillStyle = originalColor;
        ctx.fillText(text, x, y);
    }
    // Draw the text with reflection
    drawReflectedText("w3resource", 50, 100, "blue", "red");
}
</script>
</body> 
</html>

Example: An ellipse

The following example draws an ellipse where transform() method has used and scale the canvas in the appropriate direction so that a circle becomes an ellipse.

Output:

Code:

<!DOCTYPE html>
<html>
<head>
<title>Matrix Transforms - ellipse</title>
</head>
<body>
<canvas id="DemoCanvas" width="300" height="400"></canvas>
<script>
var canvas = document.getElementById("DemoCanvas");
if (canvas.getContext) 
{
 var ctx = canvas.getContext('2d');
 ctx.transform(1.6,0,0,1,0,0);
 ctx.beginPath();
 ctx.fillStyle = 'red';
 ctx.lineWidth = 4;
 ctx.arc(60, 60, 45, 0, 2 * Math.PI, true);
 ctx.stroke();
 ctx.fill();  
}
</script>
</body> 
</html>

Code Editor:

See the Pen html css common editor by w3resource (@w3resource) on CodePen.

Previous: HTML5 Canvas translation, scaling and rotation tutorial
Next: HTML5 Canvas: Compositing