NumPy array creation: vander() function

numpy.vander() function

The vander() function is used to generate a Vandermonde matrix.
The columns of the output matrix are powers of the input vector. The order of the powers is determined by the increasing boolean argument. Specifically, when increasing is False, the i-th output column is the input vector raised element-wise to the power of N - i - 1. Such a matrix with a geometric progression in each row is named for Alexandre- Theophile Vandermonde.

Syntax:

numpy.vander(x, N=None, increasing=False)

Version: 1.15.0

Return value:

out : ndarray - Vandermonde matrix. If increasing is False, the first column is x^(N-1), the second x^(N-2) and so forth. If increasing is True, the columns are x^0, x^1, ..., x^(N-1).

Example-1: NumPy.vander() function

>>> import numpy as np
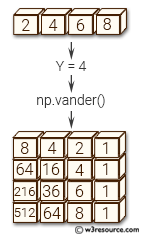
>>> a = np.array ([1,2,4,6])
>>> Y=4
>>> np.vander(a, Y)
array([[  1,   1,   1,   1],
       [  8,   4,   2,   1],
       [ 64,  16,   4,   1],
       [216,  36,   6,   1]])
>>> np.column_stack([a**(Y-1-i) for i in range(Y)])
array([[  1,   1,   1,   1],
       [  8,   4,   2,   1],
       [ 64,  16,   4,   1],   
       [216,  36,   6,   1]])

Pictorial Presentation:

Example-2: NumPy.vander() function

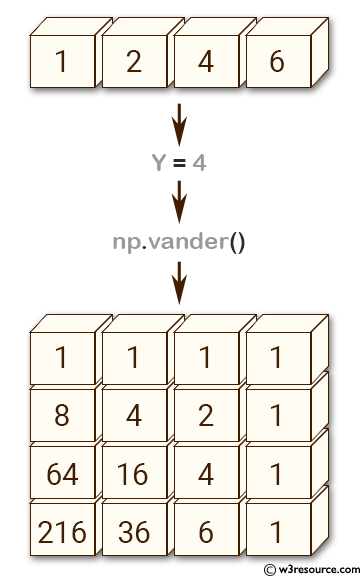
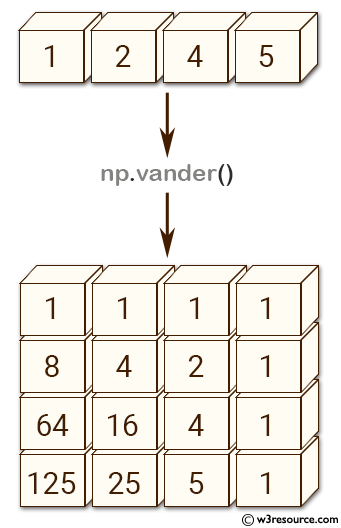
>>> import numpy as np
>>> a = np.array([1,2,4,5])
>>> np.vander(a)
array([[  1,   1,   1,   1],
       [  8,   4,   2,   1],
       [ 64,  16,   4,   1],in
       [125,  25,   5,   1]])
>>> np.vander(a, increasing=True)
array([[  1,   1,   1,   1],
       [  1,   2,   4,   8],
       [  1,   4,  16,  64],
       [  1,   5,  25, 125]])

Pictorial Presentation:

The determinant of a square Vandermonde matrix is the product of the differences between the values of the input vector:

>>> import numpy as np
>>> a = np.array([1,2,4,5])
>>> np.linalg.det(np.vander(a))
72.000000000000071
>>> (5-4)*(5-2)*(5-1)*(4-2)*(4-1)*(2-1)
72

Python - NumPy Code Editor:

Previous: triu()
Next: The Matrix class mat()