NumPy: numpy.eye() function
numpy.eye() function
The eye() function is used to create a 2-D array with ones on the diagonal and zeros elsewhere.
The eye() function is commonly used in linear algebra and matrix operations. It is useful for generating matrices to transform, rotate, or scale vectors. It can also be used in scientific computing for solving differential equations, optimization, and signal processing.
Syntax:
numpy.eye(N, M=None, k=0, dtype=<class 'float'>, order='C')
Parameters:
| Name | Description | Required / Optional |
|---|---|---|
| N | Number of rows in the output. | Required |
| M | Number of columns in the output. If None, it defaults to N. | optional |
| k | Index of the diagonal. 0 (default) refers to the main diagonal, a positive value refers to an upper diagonal, and a negative value refers to a lower diagonal. | optional |
| dtype | Data type of the returned array. | optional |
| order | Memory layout order of the output array. 'C' for row-major (C-style) and 'F' for column-major (Fortran-style). | optional |
Return value:
A 2-D array where all elements are zero except for the k-th diagonal, whose values are ones.
Example-1: Identity Matrix using NumPy eye function
>>> import numpy as np
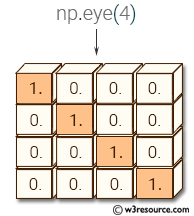
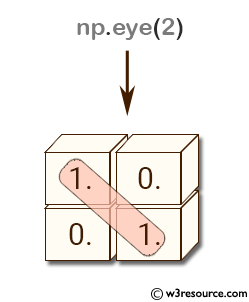
>>> np.eye(2)
array([[ 1., 0.],
[ 0., 1.]])
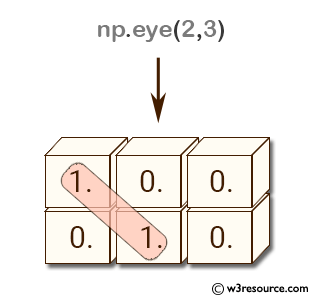
>>> np.eye(2,3)
array([[ 1., 0., 0.],
[ 0., 1., 0.]])
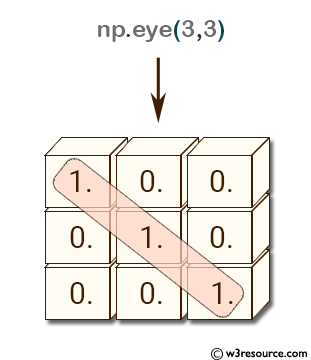
>>> np.eye(3, 3)
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
>>>
In linear algebra, an identity matrix is a square matrix with ones on the main diagonal and zeros elsewhere.
In the first example, np.eye(2) creates a 2x2 identity matrix where both the rows and columns are equal to 2.
In the second example, np.eye(2,3) creates a 2x3 identity matrix where the first argument specifies the number of rows and the second argument specifies the number of columns.
In the third example, np.eye(3,3) creates a 3x3 identity matrix where both the rows and columns are equal to 3.
Visual Presentation:
Example-2: Identity Matrix using NumPy eye function
>>> import numpy as np
>>> np.eye(2, dtype=int)
array([[1, 0],
[0, 1]])
>>> np.eye(2,2, dtype=int)
array([[1, 0],
[0, 1]])
>>> np.eye(2,2, dtype=float)
array([[ 1., 0.],
[ 0., 1.]])
>>>
In the first example, np.eye(2, dtype=int) creates a 2x2 identity matrix with integer data type. The resulting array is array([[1, 0], [0, 1]]).
In the second example, np.eye(2,2, dtype=int) creates the same 2x2 identity matrix with integer data type. The 2,2 parameter specifies the size of the matrix, and since the dtype parameter is set to int, the resulting array is the same as the first example.
In the third example, np.eye(2,2, dtype=float) creates a 2x2 identity matrix with float data type. The resulting array is array([[1., 0.], [0., 1.]])
Example: Create a sparse identity matrix with a non-zero diagonal offset:
Code:
import numpy as np
# Create a sparse identity matrix with diagonal offset of 1
nums = np.eye(5, k=1, dtype=int)
print(nums)
Output:
[[0 1 0 0 0] [0 0 1 0 0] [0 0 0 1 0] [0 0 0 0 1] [0 0 0 0 0]]
In the above example, we create a sparse identity matrix with dimensions (5, 5) and a diagonal offset of 1. This means that the diagonal elements are shifted one position to the right, resulting in a matrix with 1's on the first upper diagonal and 0's elsewhere.
Example: Create a complex-valued identity matrix with non-unit diagonal elements
Code:
import numpy as np
# Create a complex-valued identity matrix with diagonal elements of 1+1j
nums = np.eye(3, dtype=complex) * (1 + 1j)
print(nums)
Output:
[[1.+1.j 0.+0.j 0.+0.j] [0.+0.j 1.+1.j 0.+0.j] [0.+0.j 0.+0.j 1.+1.j]]
In the above example, we create a complex-valued identity matrix with dimensions (3, 3) and diagonal elements of 1+1j (i.e., the real part is 1 and the imaginary part is 1). In order to achieve this, we multiply the output of np.eye() function by the complex scalar (1+1j). The resulting matrix has diagonal elements of 1+1j and 0's elsewhere.
FAQs for NumPy eye() Function
1. What is the purpose of the numpy.eye() function?
The numpy.eye() function is used to create a 2-D array with ones on the diagonal and zeros elsewhere. It is particularly useful in linear algebra and various matrix operations.
2. In what fields is the numpy.eye() function commonly used?
The numpy.eye() function is commonly used in linear algebra, scientific computing, signal processing, optimization, and solving differential equations.
3. Can numpy.eye() create non-square matrices?
Yes, numpy.eye() can create non-square matrices by specifying different values for the number of rows and columns.
4. What does the diagonal offset parameter (k) do in numpy.eye()?
The diagonal offset parameter (k) in numpy.eye() shifts the diagonal with ones. A positive value moves the diagonal upwards, a negative value moves it downwards, and the default (zero) places it on the main diagonal.
5. Is it possible to specify the data type of the array created by numpy.eye()?
Yes, you can specify the data type of the array created by numpy.eye() using the dtype parameter.
6. How does the order parameter affect the output of numpy.eye()?
The order parameter determines the memory layout of the output array. 'C' means row-major (C-style) order, and 'F' means column-major (Fortran-style) order.
7. Can numpy.eye() be used to create identity matrices for complex numbers?
Yes, numpy.eye() can create identity matrices for complex numbers by specifying a complex data type in the dtype parameter.
8. How is numpy.eye() different from numpy.identity()?
While both numpy.eye() and numpy.identity() create identity matrices, numpy.eye() provides more flexibility. It allows specifying the number of rows and columns independently and supports diagonal offsets, whereas numpy.identity() only creates square matrices with ones on the main diagonal.
9. What happens if M is not provided in numpy.eye()?
If the number of columns (M) is not provided, numpy.eye() defaults to creating a square matrix with M equal to the number of rows (N).
Python - NumPy Code Editor:
Previous: empty_like()
Next: identity()
