NumPy: numpy.meshgrid() function

Last update on March 21 2023 12:08:47 (UTC/GMT +8 hours)

numpy.meshgrid() function

The numpy.meshgrid() function is used to get coordinate matrices from coordinate vectors.
Make N-D coordinate arrays for vectorized evaluations of N-D scalar/vector fields over N-D grids, given one-dimensional coordinate arrays x1, x2,…, xn.

Syntax:

numpy.meshgrid(*xi, **kwargs)

Parameters:

Name	Description	Required / Optional
x1, x2,…, xn	1-D arrays representing the coordinates of a grid.
indexing	Cartesian (‘xy’, default) or matrix (‘ij’) indexing of output. See Notes for more details. New in version 1.7.0.	optional
sparse	If True a sparse grid is returned in order to conserve memory. Default is False. New in version 1.7.0.	optional
endpoint	If True, stop is the last sample. Otherwise, it is not included. Default is True.	optional
copy	If False, a view into the original arrays are returned in order to conserve memory. Default is True. Please note that sparse=False, copy=False will likely return non-contiguous arrays. Furthermore, more than one element of a broadcast array may refer to a single memory location. If you need to write to the arrays, make copies first. New in version 1.7.0.	optional

Return value:

X1, X2,…, XN : ndarray - For vectors x1, x2,…, ‘xn’ with lengths Ni=len(xi) , return (N1, N2, N3,...Nn) shaped arrays if indexing=’ij’ or (N2, N1, N3,...Nn) shaped arrays if indexing=’xy’ with the elements of xi repeated to fill the matrix along the first dimension for x1, the second for x2 and so on.

Example: Create Meshgrid

>>> import numpy as np
>>> ab, ac = (4, 2)
>>> b = np.linspace(0, 1, ab)
>>> c = np.linspace(0, 1, ac)
>>> bd, cd = np.meshgrid(b, c)
>>> bd
array([[ 0.        ,  0.33333333,  0.66666667,  1.        ],
       [ 0.        ,  0.33333333,  0.66666667,  1.        ]])
>>> cd
array([[ 0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.]])
>>> bd, cd = np.meshgrid(b, c, sparse=True) #make sparse output arrays
>>> bd
array([[ 0.        ,  0.33333333,  0.66666667,  1.        ]])
>>> cd
array([[ 0.],
       [ 1.]])

In the said code, first we define two variables ab and ac to be 4 and 2 respectively. Then we create two arrays b and c using np.linspace() function which creates an array of evenly spaced numbers over a specified interval.
Next, np.meshgrid() is called with b and c as inputs, and the resulting outputs are assigned to bd and cd.
In the next part of the code, np.meshgrid() is called again with the sparse=True argument. This creates the same coordinate grid as before, but returns "sparse" output arrays, where dimensions with size 1 are squeezed out. Thus, bd is now a 1D array containing the values of b, and cd is a 1D array containing the values of c.

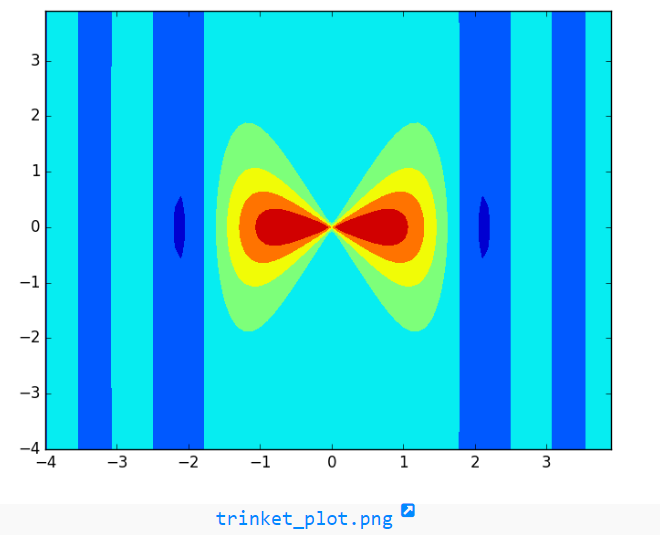
Example: Contour Plot of Sin(x^2) / (x^2 + y^2)

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> a = np.arange(-4, 4, 0.1)
>>> b = np.arange(-4, 4, 0.1)
>>> aa, bb = np.meshgrid(a, b, sparse=True)
>>> c = np.sin(aa**2) / (aa**2 + bb**2)
>>> m = plt.contourf(a,b,c)
>>> plt.show()

The above code generates a contour plot of the function sin(x^2) / (x^2 + y^2). It uses the numpy and matplotlib.pyplot libraries.

numpy.logspace.plot show

Python - NumPy Code Editor:

Previous: geomspace()
Next: mgrid()